scipy: Faster implementation of scipy.sparse.block_diag
Before making a move on this, I would like to put this potential enhancement out on GitHub to discuss, to gauge interest first. I’m hoping this discussion reveals something fruitful, perhaps even something new that I can learn, and it doesn’t necessarily have to result in a PR.
For one of my projects involving message passing neural networks, which operate on graphs, I use block diagonal sparse matrices a lot. I found that the bottleneck is in the block_diag creation step.
To verify this, I created a minimal reproducible example, using NetworkX.
Reproducing code example:
import networkx as nx
import numpy as np
from scipy.sparse import block_diag, coo_matrix
import matplotlib.pyplot as plt
Gs = []
As = []
for i in range(50000):
n = np.random.randint(10, 30)
p = 0.2
G = nx.erdos_renyi_graph(n=n, p=p)
Gs.append(G)
A = nx.to_numpy_array(G)
As.append(A)
In a later Jupyter notebook cell, I ran the following code block.
%%time
block_diag(As)
If we vary the number of graphs that we create a block diagonal matrix on, we can time the block_diag function, which I did, resulting in the following chart:

Some additional detail:
- 3.5 seconds for 5,000 graphs, 97,040 nodes in total.
- 13.3 seconds for 10,000 graphs, 195,367 nodes in total. (2x the inputs, ~4x the time)
- 28.2 seconds for 15,000 graphs, 291,168 nodes in total. (3x the inputs, ~8x the time)
- 52.9 seconds for 20,000 graphs, 390,313 nodes in total. (4x the inputs, ~16x the time)
My expectation was that block_diag should scale linearly with the number of graphs. However, the timings clearly don’t show that.
I looked into the implementation of block_diag in scipy.sparse, and found that it makes a call to bmat, which considers multiple cases for array creation. That said, I wasn’t quite clear how to make an improvement to bmat, thus, I embarked on an implementation that I thought might be faster. The code looks like such:
def block_diag_nojit(As: List[np.array]):
row = []
col = []
data = []
start_idx = 0
for A in As:
nrows, ncols = A.shape
for r in range(nrows):
for c in range(ncols):
if A[r, c] != 0:
row.append(r + start_idx)
col.append(c + start_idx)
data.append(A[r, c])
start_idx = start_idx + nrows
return row, col, data
row, col, data = block_diag_nojit(As)
Profiling the time for this:
CPU times: user 7.44 s, sys: 146 ms, total: 7.59 s
Wall time: 7.58 s
And just to be careful, I ensured that the resulting row, col and data were correct:
row, col, data = block_diag_nojit(As[0:10])
amat = block_diag(As[0:10])
assert np.allclose(row, amat.row)
assert np.allclose(col, amat.col)
assert np.allclose(data, amat.data)
I then tried JIT-ing the function using numba:
%%time
row, col, data = jit(block_diag_nojit)(As)
Profiling the time:
CPU times: user 1.27 s, sys: 147 ms, total: 1.42 s
Wall time: 1.42 s
Creating the coo_matrix induces a flat overhead of about 900ms, thus it is most efficient to call coo_matrix outside of the block_diag_nojit function:
# This performs at ~2 seconds with the scale of the graphs above.
def block_diag(As):
row, col, data = jit(block_diag_nojit)(As)
return coo_matrix((data, (row, col)))
For a full characterization:
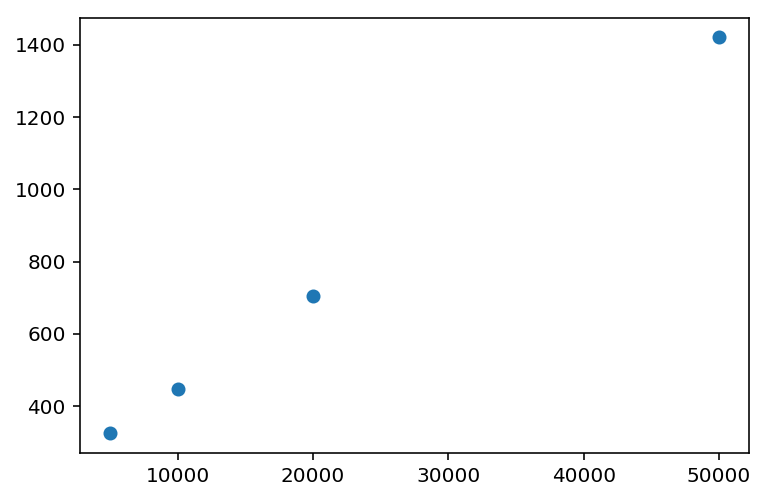
(This is linear in the number of graphs.)
I’m not quite sure why the bmat-based block_diag implementation is super-linear, but my characterization of this re-implementation shows that it is up to ~230x faster with JIT-ing, and ~60x faster without JIT-ing (at the current scale of data). More importantly, the time taken is linear with the number of graphs, and not raised to some power.
I am quite sure that the block_diag matrix implementation, as it currently stands, was built with a goal in mind that I’m not aware of, which necessitated the current implementation design (using bmat). That said, I’m wondering if there might be interest in a PR contribution with the aforementioned faster block_diag function? I am open to the possibility that this might not be the right place, in which I’m happy to find a different outlet.
Thank you for taking the time to read this!
About this issue
- Original URL
- State: closed
- Created 6 years ago
- Comments: 15 (4 by maintainers)
Hi, I am also interested in contributing to the scipy repository, and thought this was a good place to get started, thanks to the guidance from @ericmjl and @perimosocordiae. I hope it is ok if I try to tackle this issue as well. So far, I believe I have been able to reproduce @ericmjl’s findings. This is what I have:
sparse.block_diagas proposed by @ericmjl with some minor changesOriginal implementation: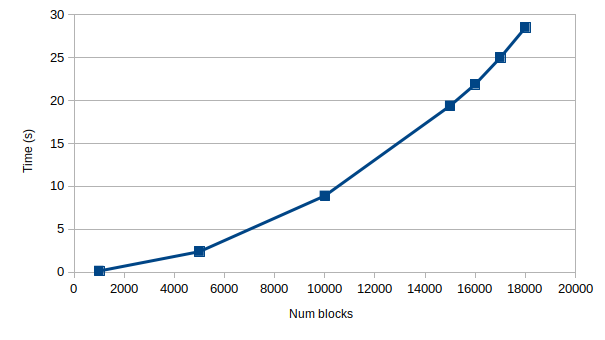 (the benchmark fails due to time out for 19 and 20 k)
(the benchmark fails due to time out for 19 and 20 k)
Proposed implementation: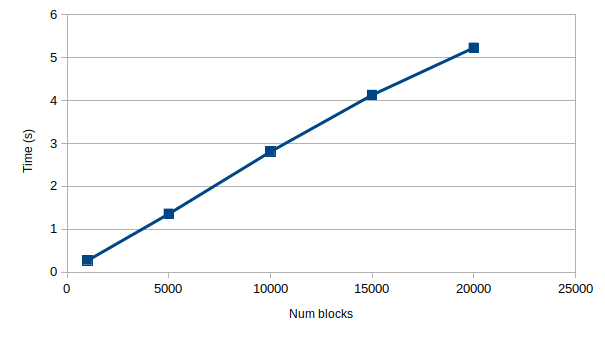
There are only three tests for this particular method, and I am not confident that I did not break anything 😃 could you please have a look at what I did and let me know if it is OK enough for a PR, or if there is anything else I should do as a next step? Thank you so much!
@ludcila wonderful work! FWIW, I also learned a thing here - didn’t realize there was a benchmarking framework!
Hi @ericmjl, thank you for the encouragement and for laying everything out so that a beginner like me can have a much better idea on where and how to start contributing 😄
Regarding the unit tests, yes, I refer to the 3 tests in the scipy test suite. I did not want to extend my previous post too much, but this is what happened: I was initially only running the test
test_block_diag_basicto verify that I was understanding the problem correctly. After I was able to pass this test, I went on to the other two tests, and realized that my implementation did not work with lists, because I was accessinga.shape. This is something I would have missed were it not for the existing tests. But just by looking at the docstring inblock_diagit was not obvious to me that it should also support lists (maybe I should have known that but I am not a regular user of scipy). I guess there could be other things that are not covered by the tests, but I am not sure what to look for 😅I will do the PR and see what feedback I get from other maintainers as well. Thank you so much!
Contributions are always welcome! A few more notes for getting started:
mastercan cause issues when merging.python runtests.py -s sparsewill build a local version from your current repo state and run thescipy.sparsetests.python runtests.py -ito get an IPython shell.Generally, as long as the function retains its API unchanged, performance improvements can be made without many restrictions.
In this case, the bad performance probably comes from the large number of blocks. It should be straightforward to write
block_diagin the same way as the inner loop ofbmat, so that it does not have to do the O(nblocks**2) loop.(Adding relevant tags.)