shapely: Getting rid of points between 'vertices' of polygons that simplify() doesn't always remove (possible alternative?)

This is kind of related to issue #939 that was previously marked invalid. And I wanted to highlight it a bit more with example pictures and also ask if there is any interest in having a similar feature implemented in Shapely?

So I find that sometimes the simplify() method with polygons doesn’t remove points that lie along the edges between vertices which can lead me into a heuristic battle trying out different tolerance values with no success (and lead me to having a similar issue as in #939, of only wanting the ‘obvious’ corners).

One of the suggestions in that issue thread though was the use of some trig along with the exterior.coords attribute. So far I’ve found this approach really handy! And it has yet to fail me (by no means robust though, I’ve only been using it on simple, non-intersecting polygons)

Example

Here is an simple example with a hexagon with a bunch of points along the edges between vertices

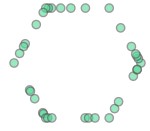
Below is an attempt using the simplify() method with preserve_topology = False

tolerance values: [1e-10, 0.1, 1, 10, 100] (left to right, respectively)

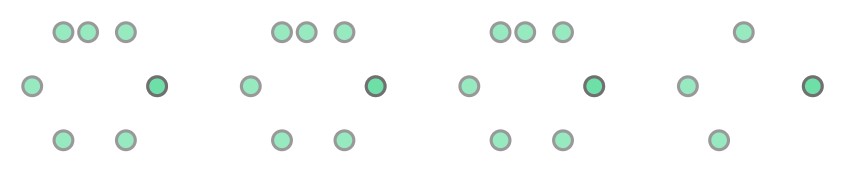
So in this example, either there was still a persistent point or too many points were removed (in the case of 100, it was completely removed). In some shapes, there could be a value between 1 and 10 which gives the correct shape as desired, but this leads me back to my previous point about getting into a heuristic battle. (and for this example however, there was no value between 1 and 10 which gave the ‘right’ result)

Repeated again, but with preserve_topology = True

Same deal as above

But with the suggested approach of using the exterior coordinates + trigonometry, I am able to get the ideal result

Code

so the basic idea is the function simplify_by_angle cycles through the coordinate sequence, constructs a vector of differences between sequential points, and then computes the angles between these vectors and eliminates anything to satisfy the degree tolerance (I use 1 degree here as an example, since I only just want to eliminate only points that lie on the straight edges between vertices).

import numpy as np
import shapely.geometry as sg

def get_angles(vec_1,vec_2):
    """
    return the angle, in degrees, between two vectors
    """
    
    dot = np.dot(vec_1, vec_2)
    det = np.cross(vec_1,vec_2)
    angle_in_rad = np.arctan2(det,dot)
    return np.degrees(angle_in_rad)


def simplify_by_angle(poly_in, deg_tol = 1):
    """
    try to remove persistent coordinate points that remain after
    simplify, convex hull, or something, etc. with some trig instead
    params:
    poly_in: shapely Polygon 
    deg_tol: degree tolerance for comparison between successive vectors
    return: 'simplified' polygon
    
    """
    
    ext_poly_coords = poly_in.exterior.coords[:]
    vector_rep = np.diff(ext_poly_coords,axis = 0)
    angles_list = []
    for i in range(0,len(vector_rep) -1 ):
        angles_list.append(np.abs(get_angles(vector_rep[i],vector_rep[i+1])))
    
#   get mask satisfying tolerance
    thresh_vals_by_deg = np.where(np.array(angles_list) > deg_tol)
    
#   gotta be a better way to do this next part
#   sandwich betweens first and last points
    new_idx = [0] + (thresh_vals_by_deg[0] + 1).tolist() + [0]
    new_vertices = [ext_poly_coords[idx] for idx in new_idx]
    

    return sg.Polygon(new_vertices)

As mentioned I only tested it with Polygon types. In terms of efficiencies it could use some work, as well as possibly removing the NumPy dependency?

by the way if anyone wanted to play around with the hexagon, here is a wkt of it

from shapely import wkt
test_hex_wkt = 'POLYGON ((30 10, 29.95 10.08660254037844, 28.7 12.25166604983954, 25.05 18.57365149746594, 24.6 19.35307436087194, 23.4 21.43153532995459, 20 27.32050807568877, 18.1 27.32050807568877, 16 27.32050807568877, 14.5 27.32050807568877, 11.3 27.32050807568877, 6.800000000000001 27.32050807568877, 3.552713678800501e-15 27.32050807568877, -4.999999999999998 18.66025403784439, -5.549999999999999 17.7076260936815, -7.749999999999999 13.89711431702998, -8.5 12.59807621135332, -9.100000000000001 11.55884572681199, -10 10, -7.650000000000001 5.929680602213139, -5.600000000000002 2.378976446696941, -3.550000000000004 -1.171727708819258, -3.000000000000004 -2.124355652982141, -0.6500000000000057 -6.194675050769005, -8.881784197001252e-15 -7.320508075688771, 6.499999999999991 -7.320508075688771, 9.19999999999999 -7.320508075688771, 9.69999999999999 -7.320508075688771, 11.49999999999999 -7.320508075688771, 14.19999999999999 -7.320508075688771, 20 -7.320508075688771, 23.3 -1.604740410711477, 23.65 -0.9985226280623696, 24.55 0.5603230987496204, 25.95 2.985194229346048, 27.15 5.063655198428702, 30 10))'
test_hex_poly = wkt.loads(test_hex_wkt)

Anyway, this became longer than I expected… so would something like this be of benefit to Shapely?

(also sorry, not sure if there’s a better place to post Feature Requests like this?)

Shapely version

using version 1.7.1