scipy: solve is very slow since #6775

Since the merge of #6775 scipy.linalg.solve has been terribly slow for anything but NRHS << N.

This is rather unfortunate because it has left solve unusable (too slow) for anything but NRHS << N. The merge done in #6775 was done primarily based on the performance comparison of gesv and gesvx for NRHS << N. Secondly, in the merge there was no reference of the used LA library, MKL, OpenBLAS, ATLAS, etc.?

Here I show a benchmark on both NRHS << N and NRHS == N which is not every corner case, but should highlight that gesvx is only useful for the former (unless precision is of utmost importance). For the case of NRHS > N the trend follows. I only show performance benchmark for OpenBLAS.

(I also think there is a bug in handling the deprecated flag sym_pos in the solve code. I.e. sym_pos redefines assume_a after its meaning has been digested.)

Reproducing code example:

This code has also been used to reproduce the following images.

from time import time as T
import numpy as np
import scipy as sp
import scipy.linalg as sl
la = sl.lapack

ITT = 25
N = np.arange(100, 1401, 50)

def performance():
    t = np.zeros([len(N), 4])
    for i, n in enumerate(N):
        print(n)
        A = np.random.rand(n, n) * 10.
        B = np.random.rand(n, 3) * 10.
        C = np.random.rand(n, n) * 10.

        t0 = T()
        for _ in range(ITT):
            la.dgesvx(A, B)
        t[i, 0] = (T() - t0) / ITT

        t0 = T()
        for _ in range(ITT):
            la.dgesv(A, B)
        t[i, 1] = (T() - t0) / ITT

        t0 = T()
        for _ in range(ITT):
            la.dgesvx(A, C)
        t[i, 2] = (T() - t0) / ITT

        t0 = T()
        for _ in range(ITT):
            la.dgesv(A, C)
        t[i, 3] = (T() - t0) / ITT

def accuracy():
    acc = np.zeros([len(N), 4])
    for it in range(ITT):
        print(it)
        for i, n in enumerate(N):
            A = np.random.rand(n, n) * 10.
            B = np.random.rand(n, 3) * 10.
            C = np.random.rand(n, n) * 10.

            x = la.dgesvx(A, B)[7]
            acc[i, 0] += ((dot(A, x) - B) ** 2).sum() ** .5

            x = la.dgesv(A, B)[2]
            acc[i, 1] += ((dot(A, x) - B) ** 2).sum() ** .5

            x = la.dgesvx(A, C)[7]
            acc[i, 2] += ((dot(A, x) - C) ** 2).sum() ** .5

            x = la.dgesv(A, C)[2]
            acc[i, 3] += ((dot(A, x) - C) ** 2).sum() ** .5
    acc /= ITT

performance()
accuracy()

Error message:

There is no error message, only bad performance.

Scipy/Numpy/Python version information:

scipy: 0.19.1
numpy: 1.13.1
OpenBLAS: 0.2.20

Here I show timings T(gesvx) / T(gesv): NRHS == 3: NRHS == N:

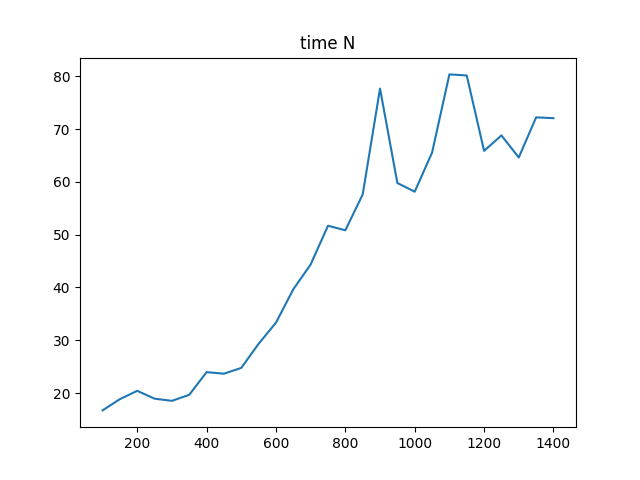
As seen the performance is really bad for NRHS == N. 80 times slower for matrices N >= 1000. I think this justifies a couple of changes to solve:

1. Revert default to gesv routines, also given the fact that gesv was the default routine in previous scipy releases.
2. Add an optional flag refine=False which determines the use of gesvx routines, if refine=True. Whether this is an appropriate name for the flag, I don’t know. If you have another idea, let me know.

If you agree to this I would be happy to contribute a PR. I have implemented a copy of solve in one of my own projects to keep using some of the functionality available in scipy, but not in numpy. You may see a re-defined solve here: https://github.com/zerothi/sisl/blob/c04ed44cbaf1ed0d485747045e4bc7cfcf9ecdfa/sisl/_numpy_scipy.py#L86 This also fixes the sym_pos flag. I.e. sym_pos has precedence. If you want a PR and you want assume_a to have precedence, I can do that as well.

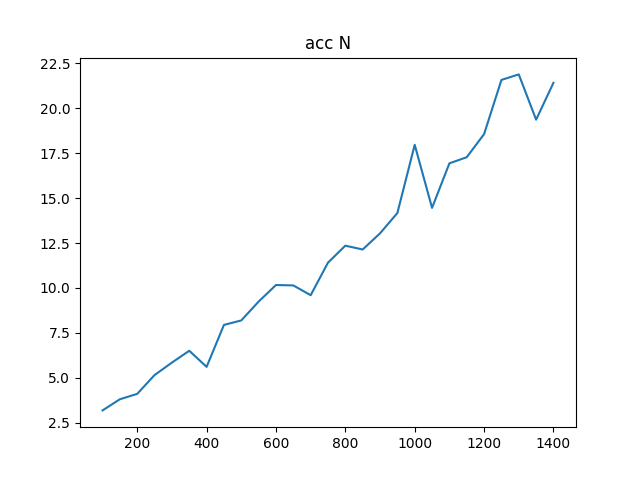
To complete the analysis I have also created an accuracy test to compare the accuracy of gesv and gesvx, they can be seen below where it is clear that gesvx is an order of magnitude more precise (given dot is numerically exact), however the Frobenius norm I would say is showing an adequate precision for this problem.
Yes, this leaves condition numbers and other analysis out of the solve routine. But currently I cannot use solve and I suspect others will also be surprised of the inferior performance since 0.19.1 (or was it 0.19.0?). As you can see in my linked solve I have added an example of how to decide whether refine is applicable for ones application.

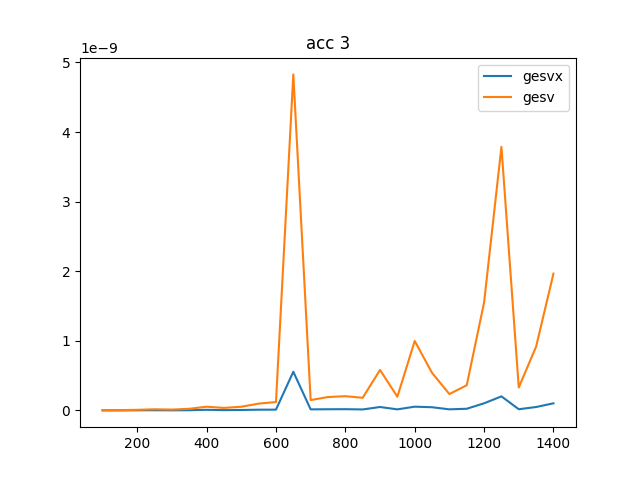
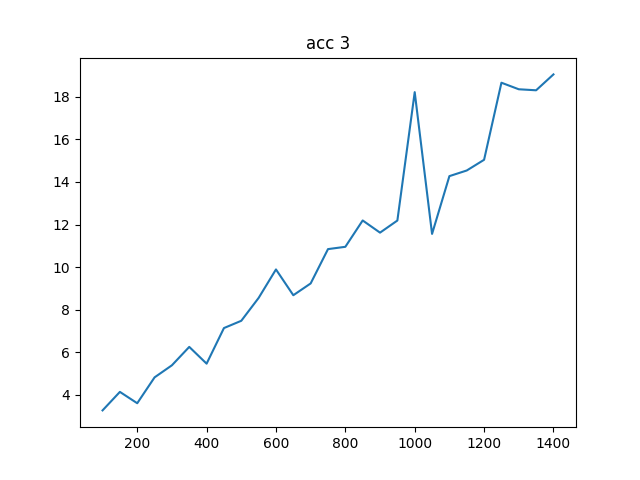
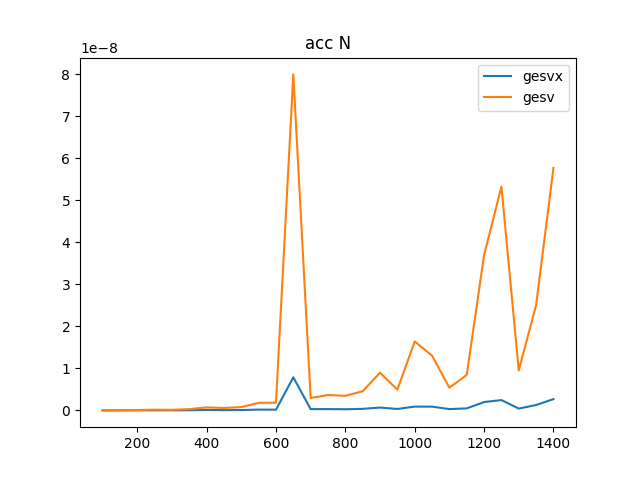
The accuracy is shown in two plots, one with the actual Frobenius norm, and one with the relative difference NRHS == 3: gesv / gesvx NRHS == N: gesv / gesvx

@ilayn, sorry for bashing your PR, your PR is most valuable! I was just surprised when I updated scipy and my code ran 50 times slower!