scipy: BUG: entropy calculations failing for large values

Describe your issue.

For a few distributions, the entropy calculation currently fails for large values. As an example, consider the gamma distribution: for $x>1e12$, the computed entropy starts to oscillate and after approx. 2e16, returns just 0.

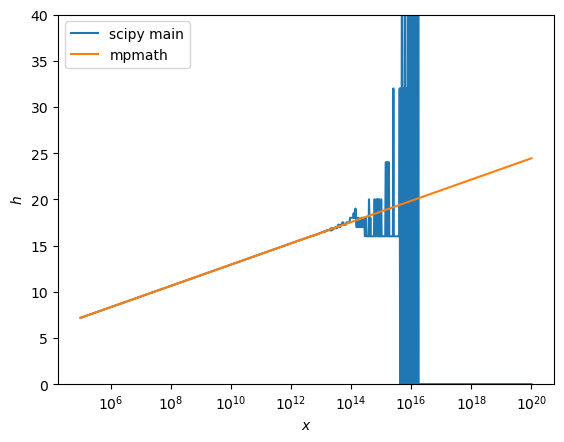
Affected distributions and current PRs that aim to fix it:

gamma #18095
gengamma #18131
invgamma #18122
f
t #18135
beta #18499 #18714
chi #18094
chi2 #17930
genlogistic #17930
wishart
invwishart
multivariate_t #18465

The reason for the failures are catastrophic cancellations occuring in the subtraction of logarithmic beta/gamma functions betaln/gammaln on one side and the digamma function psi or simply log on the other side.

This can be avoided by using asymptotic expansions instead of calling the functions from scipy.special. See #17930 for examples.

The expansions for $\psi$ and $\ln(\Gamma)$ used in PRs such as #17929 are:

$$ \begin{align} \psi(x) & \sim\ln(x) - \frac{1}{2x} - \frac{1}{12x^2}+\frac{1}{120x^4}-\frac{1}{252x^6} \
\ln(\Gamma(x)) &\sim x\ln(x)-x-\frac{1}{2}\ln(x)+\frac{1}{2}\ln(2\pi)+\frac{1}{12x}-\frac{1}{360x^3}+\frac{1}{1260x^5} \end{align} $$

For the beta function, expansions are listed on Wikipedia:

If $x$ and $y$ are large:

$$ \begin{align} B(x, y) & \sim\sqrt{2\pi}\frac{x^{x-1/2}y^{y-1/2}}{(x+y)^{x+y-1/2}} \
\ln(B(x, y)) & \sim \ln(\sqrt{2\pi})+(x-1/2)\ln(x)+(y-1/2)\ln(y)-(x+y-1/2)\ln(x+y) \end{align} $$

If one argument is large (here y, same holds for large x as betaln is symmetric):

$$ \begin{align} B(x, y) & \sim\Gamma(x)y^{-x} \
\ln(B(x, y)) & \sim \ln(\Gamma(x)) - x\ln(y) \
\end{align} $$

This issue can keep track of the necessary fixes.

Reproducing Code Example


import numpy as np
import matplotlib.pyplot as plt
from scipy import stats
from mpmath import mp

mp.dps = 50

@np.vectorize
def gamma_entropy_reference(x):
    x = mp.mpf(x)
    return mp.digamma(x) * (mp.one - x) + x + mp.loggamma(x)

x = np.logspace(5, 20, 1000)
reference_entropy = np.array(gamma_entropy_reference(x), np.float64)
plt.semilogx(x, stats.gamma.entropy(x), label="scipy main")
plt.semilogx(x, reference_entropy, label="mpmath")
plt.legend(loc='upper left')
plt.xlabel("$x$")
plt.ylabel("$h$")
plt.ylim(0, 40)
plt.show()

Error message

See plot above

SciPy/NumPy/Python version and system information

current main branch

About this issue

Original URL
State: closed
Created a year ago
Comments: 23 (23 by maintainers)

Commits related to this issue

ENH: Added asymptotic expansion for invgamma entropy (#18093) — committed to MatteoRaso/scipy by MatteoRaso a year ago
Added asymptotic expansion for t entropy (#18093) — committed to MatteoRaso/scipy by MatteoRaso a year ago

Most upvoted comments

@OmarManzoor I think the problem is that the asymptotic expansion is very wrong for digamma(a) at a=1. Only for b it should be applied here, for a the regular digamma function is correct.

dschmitz89 on Jun 16, 2023

Hi @dschmitz89

If we want to handle the beta entropy
def _entropy(self, a, b):
    return (sc.betaln(a, b) - (a - 1) * sc.psi(a) -
            (b - 1) * sc.psi(b) + (a + b - 2) * sc.psi(a + b))
do we need to consider each of the three conditions separately for the expansions as mentioned in the description i.e.

both a and b are large

a is large

b is large

Edit: I think we only need two cases. One if both arguments are large and one if only one argument is large. The formula is kind of “symmetric” so $a\to\infty$ yields the same formula as $b\to\infty$ if $a$ and $b$ are switched. CC @OmarManzoor

dschmitz89 on Jun 9, 2023

BTW technically these implementations don’t really need to use _lazywhere. It looks like if…else would work fine because the distribution infrastructure (apparently) applies np.vectorize to _entropy before it is called, so _entropy only ever gets passed scalar arguments. But go ahead and keep using _lazywhere for now; the new infrastructure will take advantage of the native vectorization. (No need for a PR or an enhancement request. I’ll track this in gh-15928, which I will address this summer,)

When this issue is ready to be closed, it would be good to take one more pass to clean up a few things:

PEP8 issues found after merge
Inconsistent use of _lazywhere. For instance, t entropy has df == np.inf: at the top, which makes it obvious that either the if statement will raise an error or _lazywhere is unnecessary. I’d suggest just removing the if statement, since the asymptotic expansion makes it unnecessary.
Ensure that overflow warnings are avoided (e.g. raise to negative powers rather than dividing by positive powers)
ValueError: Integers to negative integer powers are not allowed. are avoided
Take a look for obvious simplifications. For instance, I suggested np.log(2) + np.log(np.pi) in at least one PR because that’s how it came out of mpmath, but np.log(2*np.pi) is simpler, faster, and not in danger of causing any problems.
Take another look at the comments. There are some comments that show part of the asymptotic expansion of gammaln and psi, but not enough terms to actually derive the formula. (Additional terms were added after the comment was written, and the comment wasn’t updated.) I think it would be better to just link back to this issue or to Wolfram Alpha than to provide incomplete information.

Individually, these are mostly insignificant. But if we’re going to take the time to do all this, we might as well do it right.

mdhaber on Mar 15, 2023