scikit-learn: RidgeCV doesn't use Generalized Cross-Validation as claimed

Describe the bug

The documentation for RidgeCV says the following:

By default, it performs Generalized Cross-Validation, which is a form of efficient Leave-One-Out cross-validation.

But 1) it’s using the LOOCV not the GCV and 2) GCV isn’t “an efficient form of LOOCV”.

GCV is the leave-one-out cross-validation of a rotation of the original regression problem

X' = Q X
y' = Q y

where Q is a unitary rotation matrix

Q Q^H = I

chosen so as to circularize the matrix X' X'^H

See

Golub G., Heath M., and Wahba G., Generalized Cross-Validation as a Method for Choosing a Good Ridge Parameter (1979), TECHNOMETRICS, Vol 21, No 2

or this blog post.

There are efficient ways to compute the LOOCV, but GCV is a different metric and the rotation is designed to handle certain problem cases with performing LOOCV on X and y directly (See the cited sources for an example where LOOCV is problematic).

Steps/Code to Reproduce

We can confirm that RidgeCV isn’t using GCV by putting together an example.

1. We add some code to compute the LOOCV. (Note uses an inefficient brute-force approach for simplicity).

def compute_l_matrix(X, alpha):
    R = scipy.linalg.qr(X, mode='r')[0]
    E = np.dot(np.conj(R.T), R) + np.diag(alpha)
    return np.linalg.cholesky(E)

def compute_ridge_regression_prediction(X, y, alpha, X_test):
    z = np.dot(np.conj(X.T), y)
    L = compute_l_matrix(X, alpha)
    beta = scipy.linalg.solve_triangular(L, z, lower=True)
    beta = scipy.linalg.solve_triangular(np.conj(L.T), beta, lower=False)
    return np.dot(X_test, beta)

def compute_loocv_impl(X, y, alpha):
    result = 0
    for train_indexes, test_indexes in LeaveOneOut().split(X):
        X_train, X_test = X[train_indexes], X[test_indexes]
        y_train, y_test = y[train_indexes], y[test_indexes]
        y_pred = compute_ridge_regression_prediction(X_train, y_train, alpha, X_test)
        result += np.abs(y_test[0] - y_pred[0])**2
    return result / len(y)

def compute_loocv(X, y, alpha, fit_intercept=True):
    n, k = X.shape
    if fit_intercept:
        alpha = np.array([alpha]*k + [0])
        X = np.hstack((X, np.ones((n, 1))))
        k +=1
    else:
        alpha = np.ones(k)*alpha
    return compute_loocv_impl(X, y, alpha)

1. We add this function to compute the GCV

def compute_gcv(X, y, alpha, fit_intercept=True):
    n, k = X.shape
    if fit_intercept:
        alpha = np.array([alpha]*k + [0])
        X = np.hstack((X, np.ones((n, 1))))
        k +=1
    else:
        alpha = np.ones(k)*alpha
    U, S, Vt = np.linalg.svd(X)
    S = np.vstack((np.diag(S), np.zeros((n-k, k))))
    # Note: the rotation for GCV can be computed much more efficiently with a FFT, but this 
    # keeps things simple.
    W = np.array([[np.exp(2j*np.pi*i*j/n) / np.sqrt(n) for j in range(n)] for i in range(n)])
    X_prime = np.dot(W, np.dot(S, Vt))
    y_prime = np.dot(W, np.dot(U.T, y))
    return compute_loocv_impl(X_prime, y_prime, alpha)

Note: depending on how you treat the intercept, this function will be equivalent to this more common formula for GCV

1/n || (I - A) y ||^2 / [1/nTr(I - A)]^2
where
A = X(X^T X + n lambda )^-1 X^T

1. We load an example dataset. This is taken from

McDonald and Schwing (1973), “Instabilities of Regression Estimates Relating Air Pollution to Mortality,” Technometrics, 15, 463-481

and is available at NCSU

df = pd.read_csv('pollution.tsv', 
                 header=0, delim_whitespace=True)
X = np.array(df.iloc[:, :-1].values, dtype=float)
y = np.array(df.iloc[:,-1].values, dtype=float)
X = StandardScaler().fit_transform(X)

1. We’ll use this package to find the optimum alpha for LOOCV and GCV and verify they’re different

import peak_engines
loocv_alpha_best = peak_engines.RidgeRegressionModel(score='loocv').fit(X, y).alpha_
gcv_alpha_best = peak_engines.RidgeRegressionModel(score='gcv').fit(X, y).alpha_
print("loocv_alpha_best = ", loocv_alpha_best)
print("gcv_alpha_best = ", gcv_alpha_best)

outputs:

loocv_alpha_best =  8.437006486935175
gcv_alpha_best =  7.095235374911837

1. Plot the functions across a range of alphas.

alphas = np.arange(0.1, 20, .1)
loocv_scores = [compute_loocv(X, y, alpha) for alpha in alphas]
gcv_scores = [compute_gcv(X, y, alpha) for alpha in alphas]
plt.xlabel('Alpha')
plt.ylabel('Mean Squared Error')
plt.plot(alphas, loocv_scores, label='LOOCV')
plt.axvline(loocv_alpha_best, color='tab:green', label='LOOCV Alpha Best')
plt.plot(alphas, gcv_scores, label='GCV')
plt.axvline(gcv_alpha_best, color='tab:red', label='GCV Alpha Best')
plt.title('CV Error on Pollution Dataset')
plt.legend(loc='upper right')

outputs:

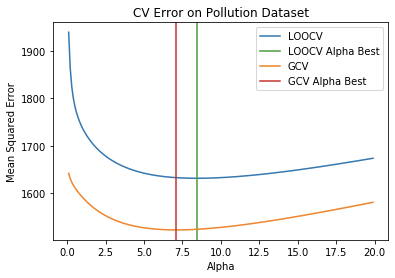
1. Build a RidgeCV model and confirm it’s using LOOCV not GCV

model = RidgeCV(list(alphas) + [loocv_alpha_best, gcv_alpha_best])
model.fit(X, y)
print(model.alpha_, loocv_alpha_best)
print(model.best_score_, compute_loocv(X, y, loocv_alpha_best))

outputs:

8.437006486935175 8.437006486935175
-1631.3585649228744 1631.3585649228833

I also put together this notebook that combines all the steps.

Expected Results

If RidgeCV used GCV as claimed, step 6 would print 7.095235374911837.

Actual Results

It printed 8.437006486935175 the LOOCV optimum.

Versions

System: python: 3.7.5 (default, Nov 20 2019, 09:21:52) [GCC 9.2.1 20191008] executable: /usr/bin/python3 machine: Linux-4.9.125-linuxkit-x86_64-with-Ubuntu-19.10-eoan

Python dependencies: pip: 18.1 setuptools: 47.1.1 sklearn: 0.23.1 numpy: 1.16.3 scipy: 1.2.1 Cython: None pandas: 0.24.2 matplotlib: 3.1.1 joblib: 0.16.0 threadpoolctl: 2.1.0

Built with OpenMP: True