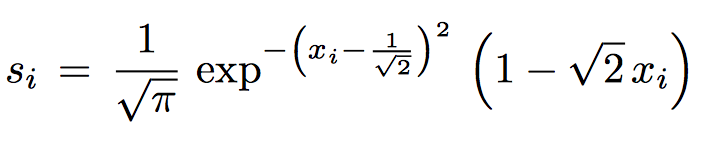LightGBM: Maybe a bug about Hessian matrix of regression_l1 objective function

Maybe a bug about Hessian matrix of regression_l1 objective function

There may be a bug in Hessian matrix of regression_l1 objective function.

It was strange and unreasonable in function ApproximateHessianWithGaussian that the gaussian variance is set as const double c = std::max((std::fabs(y) + std::fabs(t)) * eta, 1.0e-10);

The proper code maybe as const double c = std::max((std::fabs(y-t)) * eta, 1.0e-10);

Though I am not very sure if this is a bug, my program fails in weighted sampling as is reported in issue https://github.com/Microsoft/LightGBM/issues/939

reference: The Code in File: https://github.com/Microsoft/LightGBM/blob/master/src/objective/regression_objective.hpp between line 98 and line 123

  void GetGradients(const double* score, score_t* gradients,
                    score_t* hessians) const override {
    if (weights_ == nullptr) {
      #pragma omp parallel for schedule(static)
      for (data_size_t i = 0; i < num_data_; ++i) {
        const double diff = score[i] - label_[i];
        if (diff >= 0.0f) {
          gradients[i] = 1.0f;
        } else {
          gradients[i] = -1.0f;
        }
        hessians[i] = static_cast<score_t>(Common::ApproximateHessianWithGaussian(score[i], label_[i], gradients[i], eta_));
      }
    } else {
      #pragma omp parallel for schedule(static)
      for (data_size_t i = 0; i < num_data_; ++i) {
        const double diff = score[i] - label_[i];
        if (diff >= 0.0f) {
          gradients[i] = weights_[i];
        } else {
          gradients[i] = -weights_[i];
        }
        hessians[i] = static_cast<score_t>(Common::ApproximateHessianWithGaussian(score[i], label_[i], gradients[i], eta_, weights_[i]));
      }
    }
  }

And the code in File: https://github.com/Microsoft/LightGBM/blob/87fa8b542e0027e03027197ba07aab2812d6755d/include/LightGBM/utils/common.h between line 486 and line 495

inline static double ApproximateHessianWithGaussian(const double y, const double t, const double g,
                                                    const double eta, const double w=1.0f) {
  const double diff = y - t;
  const double pi = 4.0 * std::atan(1.0);
  const double x = std::fabs(diff);
  const double a = 2.0 * std::fabs(g) * w;  // difference of two first derivatives, (zero to inf) and (zero to -inf).
  const double b = 0.0;
  const double c = std::max((std::fabs(y) + std::fabs(t)) * eta, 1.0e-10);
  return w * std::exp(-(x - b) * (x - b) / (2.0 * c * c)) * a / (c * std::sqrt(2 * pi));
}

About this issue

Original URL
State: closed
Created 7 years ago
Comments: 26 (22 by maintainers)

Most upvoted comments

Btw when I run some stacking (multiple models with different hyper parameters) I always add some model with objective like above. Even for L2 (MSE) task. The reason is: this form of gradients converge to different solution and brings new variability from data. It is like “free lunch”. Almost in all datasets are some outliers pushing L2 norm to not so optimal solution (known drawback of L2). But this is little bit offtopic.

gugatr0n1c on Oct 27, 2017

Couple months ago I run some tests on this. Using gradients from {-1, 1} never worked good enough for me. I got best results for L1 task with this:

def myObj(preds, train_data): labels = train_data.get_label() grad = np.sign(preds - labels) * np.abs(preds - labels)**0.5 hess = [1.] * len(preds) return grad, hess

Because gradients only with elements from {-1, 1} are “too stupid” for this algorithm. The part: “np.abs(preds - labels)**0.5” helping algorithm to converge but it is not so aggressive as for L2. You can also run smaller exponent like: np.abs(preds - labels)**0.25

But this is only practical observation.

gugatr0n1c on Oct 27, 2017

I take some notes on approximations to the delta or step function.

Logistic Approximation to Step Function The logistic function f(x) is a smooth approximation to the step function. https://en.m.wikipedia.org/wiki/Heaviside_step_function#Analytic_approximations The derivative of f(x) is df/dx = f(x)f(1-x) = 𝞓(x), and an approximation to the delta function. https://en.m.wikipedia.org/wiki/Logistic_function#Derivative The weighting function can be defined as: W_i(y) = 𝞓((y - y_i)/T) where T is the temperature parameter. In physics, f(x) is known as the Fermi–Dirac distribution.
Methfessel-Paxton Approximation to Step Function http://www.hector.ac.uk/cse/distributedcse/reports/conquest/conquest/node6.html The N-th order approximation to the delta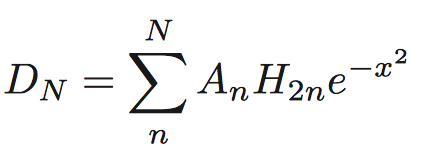 function: where A_n are suitable coefficients, and H_n are Hermite polynomials. The N-th order approximation to the step function:
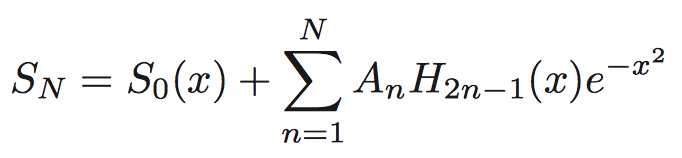
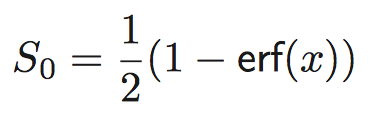
Marzari-Vanderbilt Approximation to Delta Function https://arxiv.org/pdf/cond-mat/9903147.pdf The approximation to the delta function: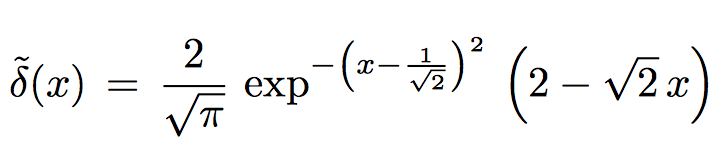 The approximation to the step function:

Tony-Y on Oct 16, 2017