LightGBM: Alpha for quantile regression doesn't seem to work

Hi there! I’ve been working with @ClimbsRocks on using auto_ml as a wrapper on top of lightgbm for a lot of our use cases at work. We’re super excited that lightgbm supports quantile regression. I saw earlier in #1036 that it looks like alpha issue was resolved, but when I pass in different alphas, I’m not seeing different results.

On my end, I wrote some functions to check if there were any difference between passing in alpha=.86 and alpha=.95 and I keep on getting results that were ~ 58th percentile as opposed to 86th or 95th on my validation and test sets.

@ClimbsRocks wrote something to test this:

%matplotlib inline
import numpy as np
import matplotlib.pyplot as plt


## ADDED
import lightgbm as lgb
## END ADDED


from sklearn.ensemble import GradientBoostingRegressor

np.random.seed(1)


def f(x):
    """The function to predict."""
    return x * np.sin(x)

#----------------------------------------------------------------------
#  First the noiseless case
X = np.atleast_2d(np.random.uniform(0, 10.0, size=10000)).T
X = X.astype(np.float32)

# Observations
y = f(X).ravel()

dy = 1.5 + 1.0 * np.random.random(y.shape)
noise = np.random.normal(0, dy)
y += noise
y = y.astype(np.float32)

# Mesh the input space for evaluations of the real function, the prediction and
# its MSE
xx = np.atleast_2d(np.linspace(0, 10, 100000)).T
xx = xx.astype(np.float32)

alpha = 0.95

# clf = GradientBoostingRegressor(loss='quantile', alpha=alpha,
#                                 n_estimators=250, max_depth=3,
#                                 learning_rate=.1, min_samples_leaf=9,
#                                 min_samples_split=9)

# clf.fit(X, y)


## ADDED
clf = lgb.LGBMRegressor(objective='quantile',
                        alpha=alpha,
                        num_leaves=31,
                        learning_rate=0.05,
                        n_estimators=100)
clf.fit(X, y,
        eval_set=[(X, y)],
        eval_metric='quantile',
        early_stopping_rounds=5)
## END ADDED


# Make the prediction on the meshed x-axis
y_upper = clf.predict(xx)

# clf.set_params(alpha=1.0 - alpha)
# clf.fit(X, y)


## ADDED
clf.set_params(alpha=1.0 - alpha)
clf.fit(X, y,
        eval_set=[(X, y)],
        eval_metric='quantile',
        early_stopping_rounds=5)
## END ADDED


# Make the prediction on the meshed x-axis
y_lower = clf.predict(xx)

# clf.set_params(loss='ls')
# clf.fit(X, y)


## ADDED
clf.set_params(objective='regression', eval_metric='l2')
clf.fit(X, y,
        eval_set=[(X, y)],
        eval_metric='l2',
        early_stopping_rounds=5)
## END ADDED


# Make the prediction on the meshed x-axis
y_pred = clf.predict(xx)

# Plot the function, the prediction and the 90% confidence interval based on
# the MSE
fig = plt.figure()
plt.plot(xx, f(xx), 'g:', label=u'$f(x) = x\,\sin(x)$')
plt.plot(X, y, 'b.', markersize=10, label=u'Observations')
plt.plot(xx, y_pred, 'r-', label=u'Prediction')
plt.plot(xx, y_upper, 'k-')
plt.plot(xx, y_lower, 'k-')
plt.fill(np.concatenate([xx, xx[::-1]]),
         np.concatenate([y_upper, y_lower[::-1]]),
         alpha=.5, fc='b', ec='None', label='90% prediction interval')
plt.xlabel('$x$')
plt.ylabel('$f(x)$')
plt.ylim(-10, 20)
plt.legend(loc='upper left')
plt.show()

and was seeing something like:

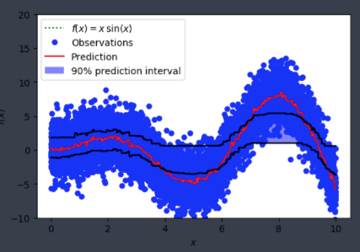
Is alpha hardcoded in somewhere or is this user error on my end?