mfem: Problems with hexahedral NC mesh

I ran @Maatinski’s code several times just to make sure we aren’t missing something and I think we’re good. To compare how NC is doing vs. the conforming code, I took the conforming mesh and forced it to be “nonconforming” in run-time with EnsureNCMesh, then compared with a regular conforming run.

The results are all expected: assembly is taking the exact same time, the only difference is in FE space setup, which is more expensive in the NC case, as is the NC mesh load (or EnsureNCMesh in this case).

I tested on a smaller mesh (test_1) with ~1M elements (the large computation wouldn’t fit on my 32G RAM machine) FE space setup was 3 sec vs 10 sec (conf vs NC) Mesh load was 3.8 sec vs 8.7 sec (conf vs NC)

I also experimented with fill_factor = 1 in CheckRehash to make the tables half-full than normal, but this didn’t have a measurable effect.

In short, NC is a little slower when creating the FE space, because a more complex P matrix needs to be set up. The extra cost is mostly the hash table operations underlying stuff like NCMesh::GetFaceList, GetEdgeList and Mesh::GeneraNCFaceInfo (when loading the mesh).

Hi Jakub, thanks for the update! Is there a certain way to order the cells and/or vertices in the mesh file to speed up generation of the hash tables? I ran some more tests in the past days using larger meshes with up to 70M children cells (i.e., not counting refined cells) and things really looked odd. Loading and initializing the meshes alone took 3-4 hours (I cannot remember the exact number) for the non-conforming meshes. I ran this on 10 MPI tasks, and the different tasks would only “ramp up” their calculations very very slowly; it almost seemed like different MPI tasks were slowing down each other, so going to more tasks actually seemed to make things worse (at least for the initialization phase). I will do some more testing on our end; I still have the feeling that my meshes might give MFEM some headache. In any case, the results are pretty impressive (see below), so I am hoping to accelerate things at least a little bit.

Mathias

That’s great news, thanks for looking into this, @jakubcerveny ! As mentioned, I have also been running larger NC meshes and the bug fix makes a huge difference. Next item on the list is to generate the NC meshes directly within MFEM which should get rid of another bottleneck… Mathias

Hi Jakub, just sent you a mail with all the needed files. Together with the meshes you already have you should be all set up. If there’s anything else I can help with let me know. Thanks and warm regards, Mathias

Hi Jakub, I will put together a minimal working example code tomorrow and send it to you… As for your suggestion to do all the meshing/refinement in MFEM: Initially I wanted to do this in Matlab to have some more control of the mesh, but especially in light of the efficiency and ability to load bigger meshes, handing this over to MFEM absolutely makes sense! I will have a look.

Mathias

That’s awesome news! Thanks a lot for looking into this, Jakub!

I ran a bunch of quick tests today: with/without the bug, and also using a conforming mesh with roughly the same number of elements (~74M) for comparison:

Mesh	Loading	Assemby	Solve
NC with bug	184.4 min	63.5 min	10.8 min
NC without bug	13.7 min	5.2 min	9.8 min
Conforming	3 min	3.9 min	23.4 min

The speed-up of the loading time was quite dramatic! Not sure why but it seems that the assembly phase (defining and constructing all the Bi-/Linear forms etc.) is also much faster now. Overall everything seems to be working fine!

@jakubcerveny Regarding the mesh generation algorithm: This is all done in Matlab. Essentially we have a Cartesian voxel model matching the spatial resolution of the smallest hex cell size we want to achieve (0.5 mm in our case). I then create an initial mesh of larger hex cells (e.g., consisting of 4x4x4 voxels), and iteratively split cells into 8 children until all cells have uniform materials (i.e., until all 0.5mm voxels belonging to that cell have the same attribute). At the end I do an additional refinement run to ensure that the size of neighboring cells vary by no more than a factor of 2. While splitting I record all vertex_parent and children information. We also do some error checking at the very end (e.g., for cyclic vertex dependencies).

This algorithm is somewhat well optimized (vectorized) but obviously still takes a couple of hours for very complex models (we’re aiming for ~200M cells), but we usually don’t need to modify these models too often. Hope this helps!

Once again, thanks for fixing this issue!! If there’s ever going to be a chance, I will owe you a beer! Mathias

I found a bug that was causing slow queries in the Node hash table. The table wouldn’t resize itself during LoadVertexParents, this is now fixed in #2781.

Overall, the load is still dominated by hash table operations (we still pay the price I was talking about), but at least loading the vertex_parents section should now scale much better. I’m hoping it could unblock Mathias’ large meshes.

I also checked the distribution of items in the tables and it looks OK.

Hi Jakub, hi all, Hope all is well with everyone at Lawrence Livermore! I finally got a chance to look into implementing @jakubcerveny 's proposed approach to generate the NC mesh “on the fly” using a material function. Once this is done, we should be ready to move these simulations to our bigger cluster (that doesn’t really have enough memory to load the whole NC mesh per node). My approach is loading the voxel model directly in MFEM and creating a coarse mesh (4x4x4) and then refining it iteratively, similarly to the shaper miniapp. The voxel model is defining an attribute per Cartesian point, with zero being background. This seems to work quite well (at the moment in serial, but I assume partitioning the coarse mesh, and then refining in parallel + re-balancing should work just as fine). The only small issue I noticed: if I start with a coarse mesh and then perform iterative refinement, I will end up with mesh cells at the boundary of the domain that have an undefined attribute. Here is an example:

The blue elements on the boundary have an attribute of zero. I assume I could simply set those to have zero conductivity (since I am solving a low-frequency quasi-static eddy-current problem), but I am not sure if this will distort the solution. In any case it will add unneeded complexity. Is there a way to remove these elements from the final mesh?

EDIT: And a second quick point: if there any easy way to enforce refinement when two neighboring coarse mesh elements have varying attributes?

Thanks a lot and warm regards, Mathias

No problem! For the mesh generation, may I recommend that you start with a 4x4x4 hex mesh, which should be SFC ordered by default (see https://mfem.org/howto/ncmesh/#load-balancing), do all the necessary refinements with MFEM in parallel (that should save a lot of time), rebalance the mesh, and save with ParMesh::ParPrint.

You should get a nice parallel mesh with N equal-sized chunks and the main code will not need to load the serial mesh N times and partition it (again saving time). One drawback is that changing N after the mesh is generated is currently not supported, but you can always regenerate for a different N.

Regarding the mesh generation algorithm

So if I understand, you have a Matlab solution that calculates the refinement structure and derives the mesh file “manually” without MFEM? That must have been non-trivial! I think a similar effect could be achieved directly with MFEM, provided the voxel material data is accessible from C++. You could start with a 4x4x4 mesh and refine it similarly as in the shaper miniapp and then just save the resulting mesh. It could even work in parallel and you could save a fully distributed mesh with ParMesh::ParPrint.

I profiled loading of @Maatinski’s mesh files and I’m afraid we can’t do much to speed up the loading of NC meshes. The extra time is all spent on creating and searching the Face and Node hash tables.

Here is an overview: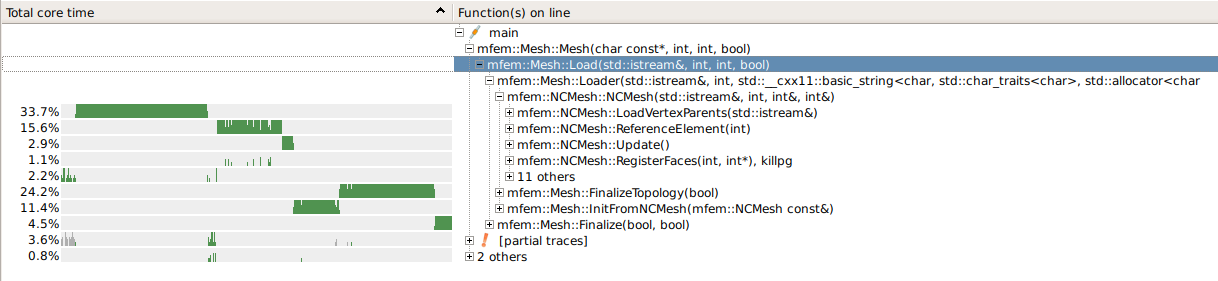

When one goes deeper it’s all mostly the HashTable (also in OnMeshUpdated and GenerateNCFaceInfo):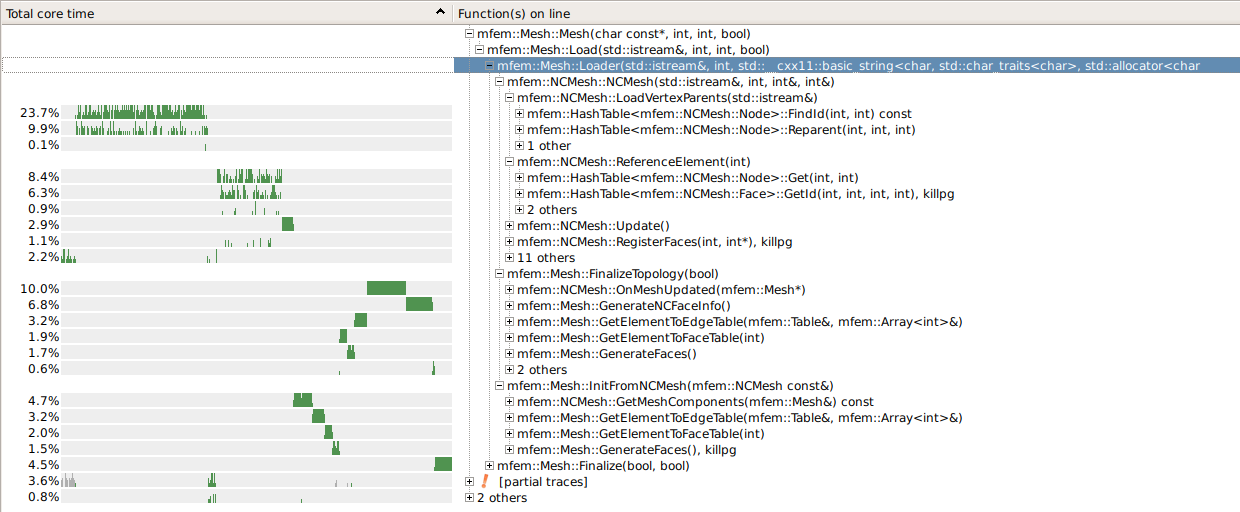

The FindId (23.7%) in LoadVertexParents could perhaps be removed (it’s just a check of the input data), but that’s probably not what we want.

I’m afraid the hashing cost is a price we pay for the simplicity and the dynamic nature of the NC algorithms.

The mesh is a bit large (1.3G, 13M elements, the two hash tables each have 32M items), going parallel is IMO the best direction here…

Hi Veselin, sorry for the missing pieces of code, but you’re exactly right! Thanks for double-checking this! Mathias

Hi Mathias,

Regarding the second question: I don’t see anything out of place. This is not in the code snippet but I assume the index gc in the call to GetVectorValue() uses the same range as cnt in the line intps[cnt] = ip; and that mpi_grid_to_cell_index[gc] is equal to mc used in the call to GetElementTransformation(). Basically, for every sample point, you determine and store the pair (mc,ip) and then you can use these pairs to sample any field on the mesh pmesh multiple times at the desired sample points. Is that correct?

-Veselin

Hi Mathias, please disregard the last comment (now deleted), I got the email. Thanks!

Hi @Maatinski

1. The NC meshes take very long to load

Do you think you could send me a minimal example showing how you are loading the meshes and ideally also the mesh files (through Google Drive, or wetransfer, or anything), so I can profile the loading code?

Thanks, Jakub

Hi @v-dobrev , thanks for the comments! I ran some first tests with bigger models and things are starting to look pretty good! I haven’t followed up on the weird effect I have seen before, as it was almost certainly an issue in my mesh (now completely gone). I do have two other quick questions though:

1. The NC meshes take very long to load

Quick summary of loading different files (all the same head “model”)

1. Conforming mesh (22.3M cells), uncompressed (2.2 GB) --> 50 sec
2. Conforming mesh (22.3M cells), gz-compressed (400 MB) --> 55 sec
3. Non-conforming mesh (11.8M cells), uncompressed (1.4 GB) --> 235 sec
4. Non-conforming mesh (11.8M cells), gz-compressed (244 MB) --> 231 sec

The mesh loading is slow for both compressed and uncompressed files. Could it be that creating the mesh representation within MFEM is slow; or is there maybe something wrong with how my NC meshes are formatted, so that MFEM needs to do a bunch of corrections?

2. Sampling the E-fields on a Cartesian grid

My second question is just to double check if I am sampling the E-field solution correctly. I am exporting the E-fields on an isotropic Cartesian grid. The NC mesh cells are pretty well structured, so for every equally spaced Cartesian grid point, I know which cell it belongs to. I am using the following code:

// cur_grid_pnt --> Grid point at which E-field is sampled
//           mc --> Index of mesh cell that contains grid point  

InverseElementTransformation *inv_tr = new InverseElementTransformation;
inv_tr->SetTransformation( *pmesh->GetElementTransformation(mc) );
IntegrationPoint ip;

int res = inv_tr->Transform(cur_grid_pnt, ip);
intps[cnt] = ip;
if ( res != 0 )
{
    MFEM_ABORT("Cannot determine integration point!");   
}      

e_->GetVectorValue(mpi_grid_to_cell_index[gc], intps[gc], vals);

The results look good, but I just wanted to make sure that I am not missing anything.

Despite these issues, the NC mesh feature is really awesome! Getting that high of a spatial resolution is becoming more critical for our modeling work. Thanks for including that feature!

Mathias