fairlearn: Error Bars/Uncertainty Quantification for MetricFrame

Is your feature request related to a problem? Please describe.

There is currently no built-in way of assessing the volatility or uncertainty associated with metrics generated via MetricFrame. This has important implications for the interpretation of any observed values or differences between groups. For example, if a metric changes significantly under small changes (e.g. through resampling), the difference might be explained fully by something like sampling error.

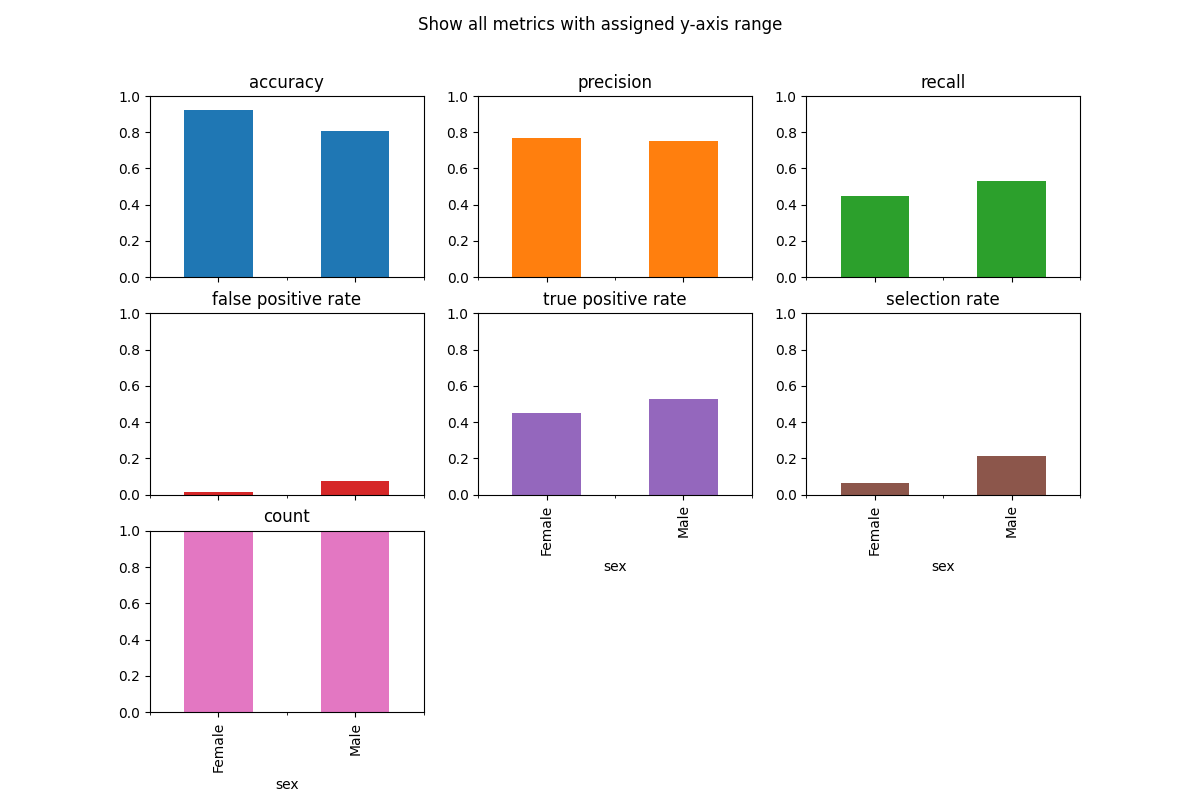
For example, here is a plot from the FairLearn documentation:

The differences between the two groups in accuracy and selection_rate appear to be larger than the differences in precision and recall. However, it could just be that metrics like selection_rate are inherently higher variance metrics than precision, which might contextualize why the magnitude of the differences is larger.

Describe the solution you’d like

I’d like to propose a bootstrap based solution built directly into MetricFrame. Bootstrap is a conceptually simple procedure that involves building an empirical distribution of a given metric/dataset by repeatedly:

1. Sampling up to the full size of the dataset with replacement
2. Re-calculating the metric on this new sample

When repeated hundreds or thousands of times, we can study the empirical distribution and produce useful summaries like confidence intervals for the metric.

There are several reasons why bootstrap might be an appropriate solution here:

• It is widely adopted and studied, making it a statistically defensible choice
• Bootstrap is agnostic to characteristics of the dataset and metric, making it largely assumption-free and widely applicable
• It is straightforward to explain and implement as a higher level layer on top of the core MetricFrame subroutines

However, it does come with a few downsides. Primarily, bootstrap is very computationally intensive. By definition, it is 100x - 1000x+ as intensive as running the core MetricFrame routine, which makes performance a key concern. This might be mitigated by:

• Having the bootstrap procedure be opt-in, and defaulted to “off”. This has the added benefit of being completely backwards compatible.
• Improving the performance of the current MetricFrame (which seems to be being addressed by PRs like https://github.com/fairlearn/fairlearn/pull/985).
• Allowing for parallel processing at the bootstrap layer, as bootstrap is an embarassingly parallel operation. This would achieve an approximately linear speedup with the number of available processes on a user machine.

Like most methods, bootstrap also does not work if the user supplied dataset is not representative of the population. In addition, bootstrap will struggle with very low sample size or incredibly homogenous groups (e.g. if every member of group A had an identical label). These should also be addressed with appropriate warnings.

Finally, it’s important to point out that error bars derived from bootstrap cannot directly be used to make claims about statistical significance, especially amongst multiple groups simultaneously. In other words, simply looking at overlaps between error bars does not constitute a formal hypothesis test.

Describe alternatives you’ve considered, if relevant

There are some alternative resampling methods that might provide tighter estimates or be slightly more computationally efficient, like the jackknife, but these are not as well known in the literature.

There is also a complementary line of work possible in structuring formal hypothesis tests, but it would supplement this contribution (and not be in place of it).

Additional context

I’d like to work on adding support for bootstrap and confidence intervals in FairLearn. I’m opening this issue to solicit community and maintainer feedback on the general idea, proposed approach, and finer details around the implementation. In addition to general comments, some thoughts on the following topics would be appreciated.

Performance / Parallel Processing

As mentioned earlier, one way to mitigate performance concerns would be to introduce parallel processing capabilities into FairLearn specifically for the bootstrap layer. Because scikit-learn is already a FairLearn dependency, we could use the joblib library to achieve this with relatively little additional code without taking on any additional dependencies. I’d just like to make sure the concept of multiprocessing and an explicit (rather than implicit) joblib dependency is OK first.

API

There’d be a few proposed changes to the MetricFrame API here, both in the input parameters to the constructor and the output data formats. Here’s an example of what the new constructor may look like (additional parameters annoted with a # NEW comment):

def __init__(self,
             *,
             metrics: Union[Callable, Dict[str, Callable]],
             y_true,
             y_pred,
             sensitive_features,
             control_features: Optional = None,
             sample_params: Optional[Union[Dict[str, Any], Dict[str, Dict[str, Any]]]] = None,
             n_boot: Optional[int] = None,  # NEW
             quantiles: Tuple[float, ...] = (2.5, 97.5), # NEW
             n_jobs: int = -1 # NEW
):

n_boot is the number of bootstrap iterations to run. This can be defaulted to None, which means skipping the bootstrap process altogether and ignoring the following parameters. In practice, it would be recommended to set this to ~1000.

quantiles are the percentiles from the empirical bootstrap distribution to preserve and report back to the user. This is defaulted to (2.5, 97.5) to represent a 95% confidence interval, but can easily be changed to an 80% interval by setting it to (10, 90). With this type of parameter specification, users can also sample more points than just the endpoints of the confidence interval – for example, if you are interested in every quartile, the API would be flexible enough to allow for e.g quantiles = (2.5, 25, 50, 75, 97.5), or to allow for asymmetric confidence intervals. We could easily drop this though and replace it with a single floating point number representing the width of the CI.

n_jobs is the popular joblib/scikit-learn parameter representing how many cores a user is willing to use on their machine for parallelization. n_jobs=1 would use a single processor, n_jobs=-1 uses every available processor, n_jobs=-2 is all but one processor, etc. More information here: https://scikit-learn.org/stable/glossary.html#term-n_jobs

In terms of output structure, there are two choices that come to mind: modifying the internals of each .by_group dataframe to hold something like a tuple instead of a scalar in each cell, or returning a separate frame for each requested quantile. I tend to prefer the latter approach, which may look something like this:

because of its readability and ease of working with – any operation or workflow established on the “main” frame would also work for the quantiles. It would be great to hear thoughts on this, and if it seems like a decent idea, how it might be exposed off the main MetricFrame object (for example, maybe mf.by_group_intervals or mf.by_group_quantiles)?

Finally, in terms of plotting, the Pandas Dataframe plotting API has support for error bars: https://pandas.pydata.org/pandas-docs/stable/user_guide/visualization.html#plotting-with-error-bars , and it might be straightforward to extend the plotting documentation to accommodate this.

Would appreciate any and all thoughts! -Harsha