xgboost: rank:ndcg does not work in Python

Hey,

rank:ndcg produces constant results, while rank:pairwise works as expected.

import numpy as np
import pandas as pd
import random
import xgboost as xgb

# creating some artificial ranking data

gsizes = [10, 100, 50]
params = [1, 2, 3]
relevances = []
features_1 = []
features_2 = []
qids = []
for gsize, param in zip(gsizes, params):
    
    range_ = list(range(gsize))
    random.shuffle(range_)
    
    relevances.extend(np.abs(np.random.randn(gsize)) + param*np.array(range_))
    feature_1 = np.array(range_)*param*2+14 + np.random.randn(gsize)
    feature_2 = np.array(range_)*param**2 + np.random.randn(gsize)**2
    features_1.extend(feature_1)
    features_2.extend(feature_2)
    qids.extend([param]*gsize)

ranker = xgb.XGBRanker(objective='rank:ndcg',
                       base_score=0.1,
                       verbosity = 1,
                       n_estimators=200)
inputs = np.array([features_1, features_2, qids]).T
fitted = ranker.fit(X=inputs , y=relevances, group=gsizes)
fitted.predict(inputs)[:10]

array([-0.9008925, -0.9008925, -0.9008925, -0.9008925, -0.9008925,
       -0.9008925, -0.9008925, -0.9008925, -0.9008925, -0.9008925],
      dtype=float32)

The results when I use pairwise:

fitted.predict(inputs)[:10]
array([-4.8152976 , -1.3937551 ,  0.36378622,  1.7936848 , -2.8243895 ,
       -9.020457  , -7.9117856 ,  3.2185328 , -7.152711  , -3.2654085 ],
      dtype=float32)

which has an NDCG of 1.

Environment: Python 3.7.6 xgboost 1.2.0

Best,

Pascal

About this issue

Original URL
State: closed
Created 4 years ago
Comments: 16 (8 by maintainers)

Most upvoted comments

Hello, when fiddling with xgboost’s Python API on MacOS, I’ve noticed a peculiar behaviour.

If, using this data, I change the relevance labels 1 into 33, effectively introducing overflows in NDCGLambdaWeightComputer::ComputeDeltaWeight and in IDCG calculation (rank_obj.cu file), rank:ndcg suddenly starts working OK, achieving NDCG@60 == 1.0 in the first iteration with default parameters, while rank:pairwise needs two iterations for the same result.

However, if I place a usleep(10) after the delta calculation (between L366 and L367 in rank_obj.cu), rebuild the lib and install the Python package, rank:ndcg works just as with labels < 32 (less than because 32 results in 0.0 IDCGs), achieving only 0.81546 after two iterations, while rank:pairwise gets 1.0. Originally, I placed a LOG(DEBUG) there to print the calculated weights but it turns out that anything somewhat time consuming is enough, a usleep(10), for example.

This behaviour is not present on a Linux VM on Google Compute Engine and rank:ndcg’s behaviour is consistently worse than rank:pairwise throughout the positive label value range, with or without the usleep(10).

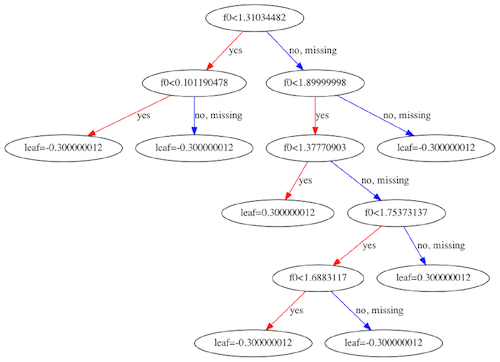
I’ve also noticed that, if not exploiting the overflow on Mac, somewhat unorthodox parameter choice can be made for rank:ndcg to perform on par with rank:pairwise in the attached example, e.g. "min_child_weight": 0.0, "lambda": 0.0 in params parameter of xgb.train(...) function. Maybe it’s due to the considerably smaller gradients of rank:ndcg compared to rank:pairwise? When rank:ndcg works on par with rank:pairwise (intentional overflow on Mac or certain min_child weight and lambda parameter choice), the trees are much more complex than in the other case.

Please find two example trees attached below - one is very simple and is a result of applying the default parameters and relevance labels. The more complex one is a result of the 2^label overflow but a similar tree is produced with particular parameter values.

The Python code I’m using:

import xgboost as xgb
import matplotlib.pyplot as plt

def train(dm, objective):
    model = xgb.train(params={
     "objective": objective,
     "eval_metric": ["ndcg@60"],
     "seed": 42,
     "verbosity": 1,
     "booster": "gbtree",
     "tree_method": "hist"
     },dtrain=dm, 
       num_boost_round=2,
       evals=[(dm,"train")],
       verbose_eval=True,
       maximize=True)
    
    return model

dm = xgb.DMatrix("dataset.libsvm")

mod_ranknet = train(dm, "rank:pairwise")
mod_lambdarank = train(dm, "rank:ndcg")

fig, ax = plt.subplots(figsize=(30, 30))
xgb.plot_tree(mod_lambdarank, num_trees=0, ax=ax)
plt.show()

Simple tree: lambdarank_narrow Complex tree: lambdarank_wide-kopia

sadaharu-inugami on Dec 18, 2020

@trivialfis could you expand on that? I know it is common to have integer labels, but float labels should work as well. Gain = 2 ^ rel_i - 1 also works for real valued relevance scores.

PascalIversen on Dec 2, 2020

hcho3 on Nov 17, 2020

Also @trivialfis any idea when the PR will be merged?

ruthlee on Jan 28, 2022

Yes. But I’m revising ndcg implementation and will submit a PR in this few days, which will be much simpler. So I suggest you to wait a bit. Will post the link to code later as I’m currently replying on phone.

trivialfis on Dec 2, 2020

Thanks for submitting the issue. Let me take a look tomorrow. The implementation involves sampling to reduce time complexity so might take some time to debug.

trivialfis on Nov 11, 2020