amgcl: Stokes problem gives NaN by AMG but GMRES works fine
I’m trying to use AMGCL to solve a simple Stokes problem using finite element method. The linear system is similar to Naiver-Stokes one:
[K G * {u = {b_u D S] p} b_p}
2nd Order FEM System size: 4080 x 4080 u is the unknows for velocity from 1 - 3600 p is the unkonws for pressure from 3601-4080
Tets=48 (I tried larger mesh which still gives me the similar error)
G and D are non-square. S has zero-diagonal. This is a typical saddle-point problem matrix for Stokes.
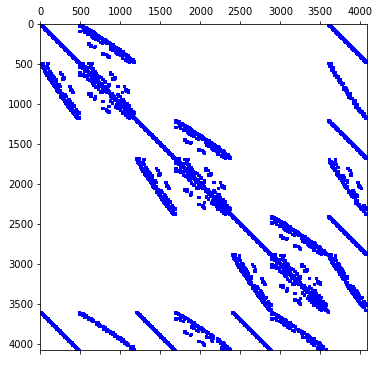
Download the linear system here Ab_mm.zip
Based on the benchmark problem, I trying to solve the system using following solver
- GMRES + ILU0, GOOD
- AMG + ILU0 and, NAN
- Schur Pressure AMG. Crash
But only 1) GMRES + ILU0 wokrs, any AMG solver return nan or Crash.
Can you check why AMGCL is not working here?
Thanks, Bin
output info:
Solver
======
Type: FGMRES(30)
Unknowns: 4080
Memory footprint: 1.94 M
Preconditioner
==============
Number of levels: 2
Operator complexity: 1.01
Grid complexity: 1.02
Memory footprint: 6.88 M
level unknowns nonzeros memory
---------------------------------------------
0 4080 201072 6.85 M (98.77%)
1 71 2503 37.69 K ( 1.23%)
#Iters=1000 Error=nan
My solver set up are:
typedef amgcl::backend::builtin<double> Backend;
//Simple iterative solver GMRES + ILU0
typedef amgcl::make_solver<
relaxation::as_preconditioner<Backend, relaxation::ilu0>,
solver::fgmres<Backend>
> Solver1;
//AMG + ILU0
typedef make_solver<
amg<Backend, coarsening::smoothed_aggregation, relaxation::ilu0>,
solver::fgmres<Backend>
> Solver2;
//Parameter setup
Solver::params prm;
double tol = 1e-6;
prm.solver.tol = tol;
prm.solver.maxiter = 1000;
//Solve the system
Solver solve(A,prm);
std::cout << solve << std::endl;
int iters;
double error;
std::tie(iters, error) = solve(b, X);
printf("#Iters=%d Error=%lf\n", iters, error);
Specially my schur_pressure_correction are:
typedef make_solver<
preconditioner::schur_pressure_correction<
make_solver<
relaxation::as_preconditioner<Backend, relaxation::damped_jacobi>,
solver::bicgstab<Backend>
>,
make_solver<
amg<
Backend,
coarsening::smoothed_aggregation,
relaxation::ilu0
>,
solver::fgmres<Backend>
>
>,
solver::fgmres<Backend>
> Solver;
//Parameter setup
Solver::params prm;
double tol = 1.0e-6;
prm.solver.tol = tol;
prm.precond.usolver.solver.tol = tol * 10;
prm.precond.psolver.solver.tol = tol * 10;
prm.precond.psolver.solver.maxiter = 1000;
prm.precond.usolver.solver.maxiter = 1000;
for(size_t i=0;i<rows;++i)
if(i>3600) prm.precond.pmask[i] = 1;
//Solve the system
Solver solve(A,prm);
std::cout << solve << std::endl;
int iters;
double error;
std::tie(iters, error) = solve(b, X);
printf("#Iters=%d Error=%lf\n", iters, error);
About this issue
- Original URL
- State: closed
- Created 4 years ago
- Comments: 61 (40 by maintainers)
Sorry about the confusion. The system is a “bad” system where the boundary condtions are not propertely setup. The V5 works fine now after fixing the boundary condition. I will post my latest benchmark soon.
I see. Well, I am out of ideas then. The approach that works (SchurPC with dummy preconditioner for the pressure part) is not strictly multigrid, so I guess the increase in the number of iterations is not unexpected. You can try to increase the number of iterations for the pressure solver (since the unpreconditioned solver is not a very effective one). It somewhat helps with the matrix you provided:
Another thing to try is to disable the use of approximate schur complement:
Finally, since the pressure part in the condensed matrix does have a nonzero diagonal, you can replace dummy preconditioner with some simple single level one like spai0 or damped_jacobi:
Not sure how any of these will scale though.
Also, the USolver and PSolver template parameters for the
schur_pressure_correctionare in the wrong order. The following works for me (I’ve changed the inner iterative solvers tobicgstabas that is what was used in my example above):The result is: